Guest blog on fundamental constants
•
Amy's note: There was uncertainty whether or not the requirements for the redefinition of the kilogram would be met by July 2017. This had consequences for as well as the metrology community, as well as The State of the Unit .
299792458 Step Aside, Here Comes—662607015!
by Michael Trott
- The definitions of the SI base units, now and in 500 days
- The long road to 6.62607015
- The carbon atom lost out
- The world of physical constants
It is going to happen:
In May 2019, the definitions of the base units of the SI system will change. Most importantly for the "State of the Unit", the kilogram will no longer be defined through the International Prototype, the magical platinum-iridium cylinder, kept safely in Paris since 1889.
Rather taking two of the 20th century physics most iconic formulas, Einstein's E = m c2 and Planck's E = h f literally and at face value and assigning a fixed exact value for h (Planck's constant), mass values are, at least conceptually, reduced to frequency measurements, ie. time.
A paper (manuscript accepted online 20 October 2017) that will probably be cited many times in years to come, titled "The CODATA 2017 Values of h, e, k, and NA for the Revision of the SI" was published (https://doi.org/10.1088/1681-7575/aa950a). Table 3 of the paper gives the exact value for the Planck constant: h =6.62607015×10-34 J·s. No uncertainty attached, an exact value of the Planck constant that implicitly defines the SI unit of mass, the kilogram. The same publication gives exact values for the Boltzmann constant, the Avogadro constant, as well as the electron charge. These four exact values constant complement the already exact value for the speed of light: c =299792458 m/s.
CODATA (Committee on Data of the International Council for Science) includes a task group on Fundamental Physical Constants, who publishes every few years the recommended values for physical constants. The most recent complete set was published 2015 (http://arxiv.org/abs/1507.07956v1). The new values for the Planck constant h (and e, k, and NA ) are the result of publications accepted by July 1, 2017.
662607015 is a number to remember. Somewhere there is now a lucky person, born in in Louisiana, lucky because the digits of his/her Social Security number match the exact value of the Planck constant. And now is the time to get an email address with the new value of the Planck constant, such as 6.62607015times10tominus34js@gmail.com before somebody else does it. But I am digressing.
The definitions of the SI base units, now and in 500 days
Right now, the seven base units of the SI are defined as follows, referencing the SI brochure [ https://www.bipm.org/en/publications/si-brochure/ ]:
The second is the duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom.
The meter is the length of the path travelled by light in vacuum during a time interval of 1/299 792 458 of a second.
The kilogram is the unit of mass; it is equal to the mass of the international prototype of the kilogram.
The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed 1 metre apart in vacuum, would produce between these conductors a force equal to 2 × 10−7 newton per metre of length.
The kelvin, unit of thermodynamic temperature, is the fraction 1/273.16 of the thermodynamic temperature of the triple point of water.
The mole is the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon 12.
The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency
540 × 1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian.
The candela is probably the last known of the seven base units of the SI. At the same time, it is the most anthropomorphic unit. The second, the meter and the kilogram are all units of time, length, and mass that represent durations, length, and masses relevant to human life. The candela serves to bridge energy with the sensitivity of the human eye.
In 2019, the new definitions for the seven base units of the SI will be something like the following (quoting from the draft of the new SI brochure https://www.bipm.org/utils/common/pdf/si-brochure-draft-2016b.pdf ):
The second, symbol s, is the SI unit of time. It is defined by taking the fixed numerical value of the caesium frequency ΔνCs , the unperturbed ground-state hyperfine transition frequency of the caesium 133 atom, to be 9 192 631 770 when expressed in the unit Hz, which is equal to 1/s
The meter, symbol m, is the SI unit of length. It is defined by taking the fixed numerical value of the speed of light in vacuum c to be 299792458 when expressed in the unit m/s, where the second is defined in terms of the caesium frequency ΔνCs .
The kilogram, symbol kg, is the SI unit of mass. It is defined by taking the fixed numerical value of the Planck constant h to be 6.626 070 015 ×10–34 when expressed in the unit J·s, which is equal to kg m2 /s where the meter and the second are defined in terms of c and ΔνCs .
The ampere, symbol A, is the SI unit of electric current. It is defined by taking the fixed numerical value of the elementary charge e to be 1.602176634×10–19 when expressed in the unit C, which is equal to A s, where the second is defined in terms of ΔνCs .
The kelvin, symbol K, is the SI unit of thermodynamic temperature. It is defined by taking the fixed numerical value of the Boltzmann constant k to be 1.380649 ×10–23 when expressed in the unit J/K, which is equal to kg·m2 /(s2·K), where the kilogram, meter and second are defined in terms of h, c and ΔνCs .
The mole, symbol mol, is the SI unit of amount of substance of a specified elementary entity, which may be an atom, molecule, ion, electron, any other particle or a specified group of such particles. It is defined by taking the fixed numerical value of the Avogadro constant NA to be 6.02214076 ×1023 when expressed in the unit 1/mol.
The candela, symbol cd, is the SI unit of luminous intensity in a given direction. It is defined by taking the fixed numerical value of the luminous efficacy of monochromatic radiation of frequency 540 ×1012 Hz, Kcd , to be 683 when expressed in the unit lm/W, which is equal to cd sr/W, or cd sr/(s3 kg m2 ), where the kilogram, meter and second are defined in terms of h, c and ΔνCs .
In addition, the new definitions are more detailed and definitely inspire readers more than ever to get at least a master’s degree in physics.
The long road to 6.62607015
These new definitions are the culmination of decades of scientific work. The two main new features of these definitions are
a) all of the SI base units are defined through physical constants, realizing after nearly 150 years James Clerk Maxwell dream how units should be defined
and
b) the kilogram, will be defined through an exact value of the Planck constant instead of being the last unit defined through a material artifact. This will eliminate the dependence of the world's system of units on the Platinum-Iridium cylinder that might change long-term up to 50μg per century (≈15fg/day).
In 1991 Terry Quinn wrote [ https://doi-org.proxy2.library.illinois.edu/10.1109/TIM.1990.1032888 ] "The domain of mass measurement, having been very quiet for much of the past one hundred years, has now awakened to the challenges presented by new physics and we can expect some exciting developments to take place over the next decade. Although we may not have a new definition of the kilogram by the year 2000 ... ." But, as it seems right now, we will have by 2020.
Only half a year ago, Amy was wondering if she would have to change the ending part of her script of the "State of the Unit". In 2013, the CCM (Consultative Committee for Mass and Related Quantities) wrote conditions that should be fulfilled for a redefinition of the kilogram through the Planck constant [ http://bipm.org/utils/common/pdf/CC/CCM/CCM14.pdf The first two being:
1. Consistency:
‘at least three independent experiments, including work from Watt balance and XRCD experiments, yield consistent values of the Planck constant with relative standard uncertainties not larger than 5 parts in 10-8 ,’
2. Uncertainty:
‘at least one of these results should have a relative standard uncertainty not larger than 2 parts in 10-8 ’,
And just half a year ago, in the meeting notes of the 16th meeting of the CCM [ https://www.bipm.org/utils/common/pdf/CC/CCM/CCM16.pdf ] one could read that it was the position of the PTB (the German national metrology institute) that these conditions were not fulfilled and that the redefinition should be postponed to 2023. Other participants considered the conditions had been met (only) "in spirit".
But with the exact values proposed by CODATA the path is open to redefine the kilogram.
And a week after the CODATA value for the Planck constant was published, at the 106th meeting CIPM (International Committee for Weights and Measures), held 26-28 October 2016, decision CIPM106/10 [ https://www.bipm.org/utils/en/pdf/CIPM/CIPM2017-Decisions-EN.pdf ] was issued, which says:
"The CIPM noted that the agreed conditions for the redefinition are now met and decided to submit Draft Resolution A to the 26th meeting of the General Conference on Weights and Measures (CGPM) and to undertake all other necessary steps to proceed with the planned redefinition of the kilogram, ampere, kelvin and mole."
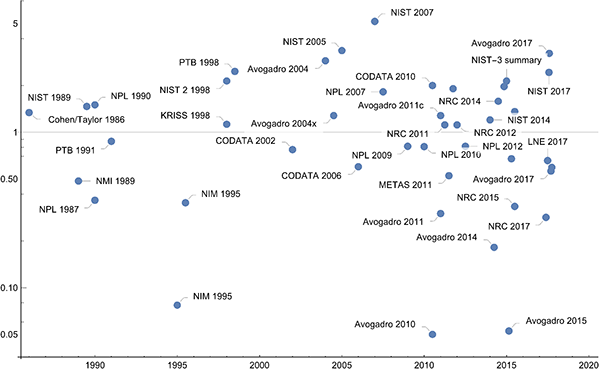
The story of the Planck constant goes back to Max Planck and the year 1900. At this time the estimated value was 6.55 10-34 J·s. Plotting the difference of historic values (measurements and summarized values) versus the new exact CODATA value over the last century shows how measurement science progressed. (This plot ignores the uncertainties of the values for the Planck constant.)
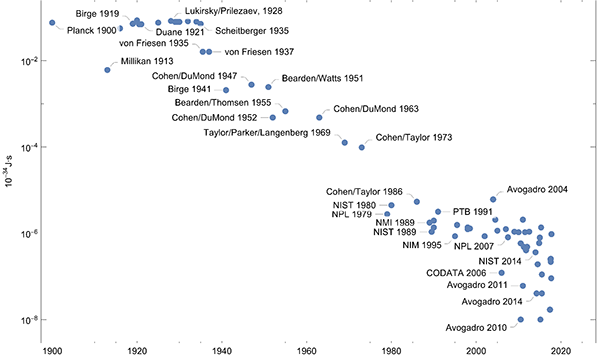
Plotting the ratios of the uncertainties to the value of the Planck constant over the years gives a similar picture.
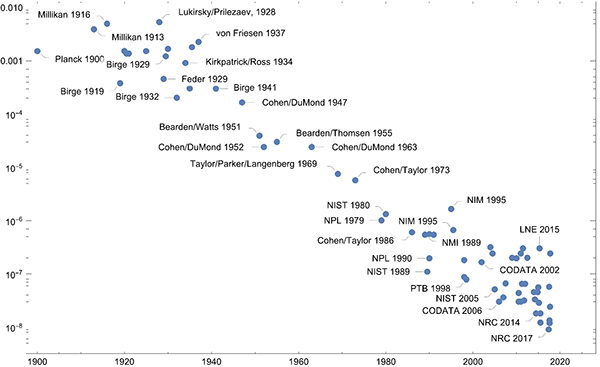
On a nonlinear scale, the progress over the last 20 years with Kibble balances and the Avogadro project stand out as achieving exceptional precision.
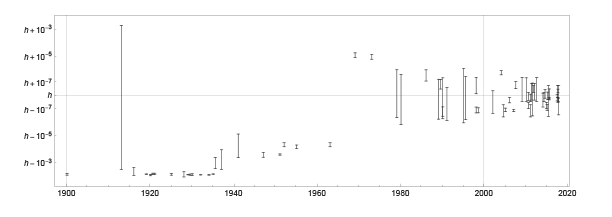
The new exact value of the Planck constant is the result of a complicated calculation that takes into account many measurements of many physical constants and tries to minimize over least squares [ https://doi.org/10.1088/1681-7575/aa99bc ]. But just taking only the various measurements of the Planck constant together constitutes an interesting mathematical problem of knowledge pooling of different probability distributions. A simple, intuitive, and theoretically well-founded method to unite different measurements is called conflation [ https://arxiv.org/abs/1005.4978 ]. The different Planck constant value measurements from the last century, shown in the plot above, give (6.62607014±0.00000003) 10-34 J·s, nearly coinciding with the CODATA value (6.62607015±0.000000069) 10-34 J·s, before rounding to the new exact value.
In the ideal case, the uncertainty of a measurement result is so large that with 68% probability the true value is included. The following graphic shows the difference to the new exact value of the Planck constant versus the uncertainties. All values above the gray line have an uncertainty so the intervals [value-uncertainty, value+uncertainty] include the next exact value. One sees that over the years also many results were published for which this was not the case.
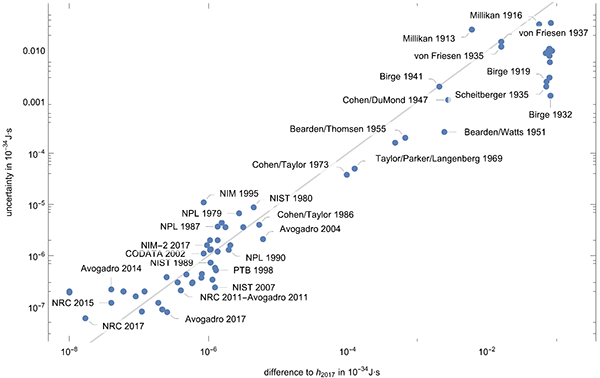
Plotting the ratio of the difference of the published mean values to the new value of the Planck constant divided by the uncertainty gives the following plot.
The concrete exact value of the Planck constant has some amusing consequences. While we are used to the speed of light being an exact integer (when measured in meters per second), due to the fact that many of the named physical constants are are products of powers of the Planck constant, the speed of light, the electron charge, the Boltzmann constant, and the Avogadro constant, large exact rational values for some constants arise. The ideal gas constant will have the exact value 8.31446261815324 J·K/mol.
The Josephson constant 2 e / h is now a rational number, in reduced terms 21362355120000000000000/44173801 Hz/V. This is a periodic decimal fraction with the nonrepeating initial digits 48 and then a period of length 6,310,542 digits. The von Klitzing constant h / e2 will have an even longer period, it is 69,313,365,540,108.
The definition of a temperature unit through the Boltzmann constant is only natural taking into account the relation between energy and temperature
And decoupling the mole from a mass unit nearly enforces the use of the Avogadro constant. A recent report of the International Union of Pure and Applied Chemistry states: [ https://doi.org/10.1515/pac-2016-0808 ]
"The total count ... shows that a majority is not satisfied with the current definition of the unit mole. A slight majority is in favour of the new definition as being proposed in the new SI."
The carbon atom lost out
The use of the Planck constant to define the mass unit and the electron charge to define the electric current are more interesting. Quite recently [ https://arxiv.org/abs/1510.08324 , https://doi.org/10.1007/s11018-017-1250-z ] alternative systems were discussed.

Here μ0 is the magnetic constant and mu is the atomic mass constant (the mass of a carbon 12 atom). Especially system E was considered to be attractive as it would define the mass unit kilogram through the mass of an atom. In such a system, the definition of a kilogram would read something like:
The kilogram is the mass of 5.018 45014 ×1025 free C12 atoms at rest and in their ground state.
The magnetic constant (also called the permeability of free space), that right now has the value 4π × 10−7 H/m would have also had a (different) exact value in system E ; it will have an approximate value in the new SI, namely μ0 = 2α/ c h / e2 where α is the fine-structure constant. And in system E the Planck constant would have continued to be a measured quantity.
The world of physical constants
There are about 22 physical constants (http://www.livingreviews.org/lrr-2011-2) related to standard model of particle physics. From these, one can form various compound physical constants. Adding temperature-related constants and some that characterize the solar system, one has about 200 constants and natural units that are in use in the natural sciences. Ignoring the constants containing candelas in their units, one can naturally embed all constants in a six-dimensional space spanned by the vectors of the base dimensions. A relatively new method to project points from higher dimensional spaces into the plane is the t-distributed stochastic neighbor embedding [ https://en.wikipedia.org/wiki/T-distributed_stochastic_neighbor_embedding ]. For the physical constants, the following plot is obtained. The physical constants that just got exact values (and the two constants already in use to define the second and the meter) are shown in red.
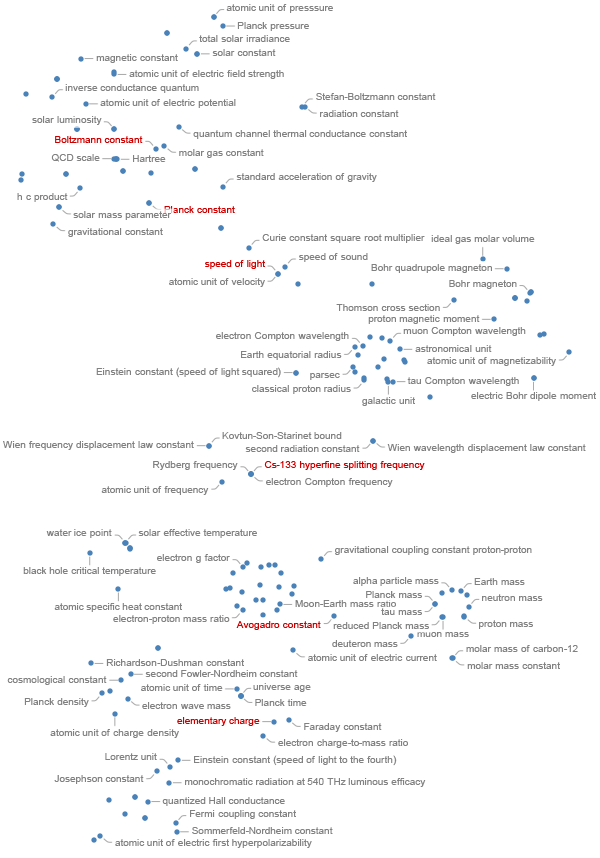
It is quite remarkable that within half a year, an agreement of the values for the Planck constant from measurements of the various groups has been achieved. It will be interesting to see how farther experiments over the next year will align with the current numbers. And kudos to the NRC team for achieving such a small uncertainty!